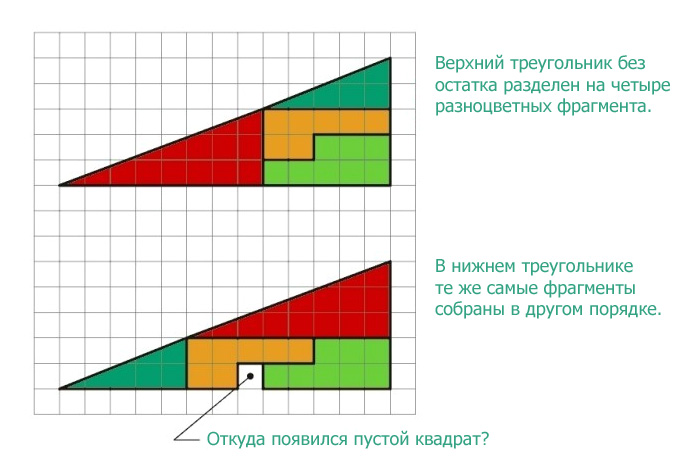
Задачка на сообразительность: откуда появился лишний пустой квадрат

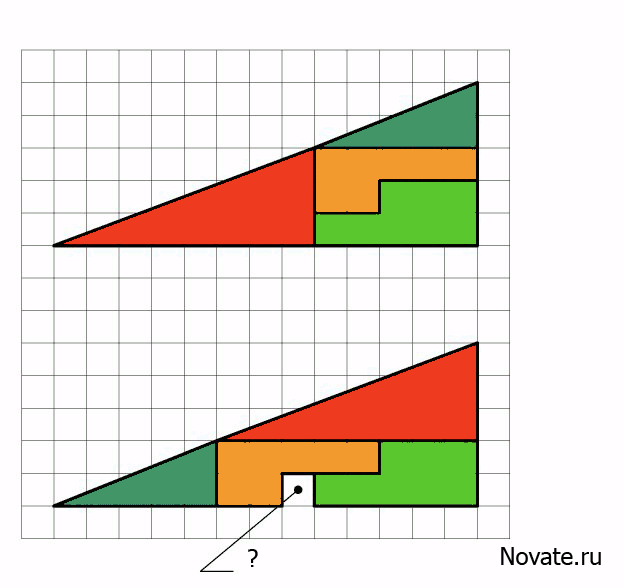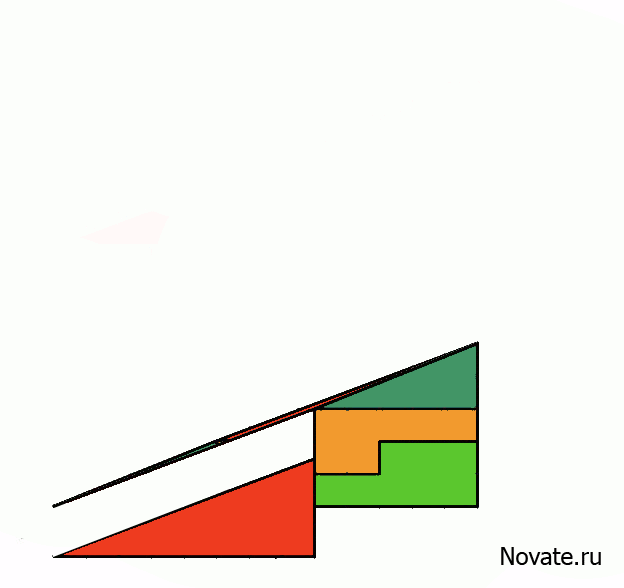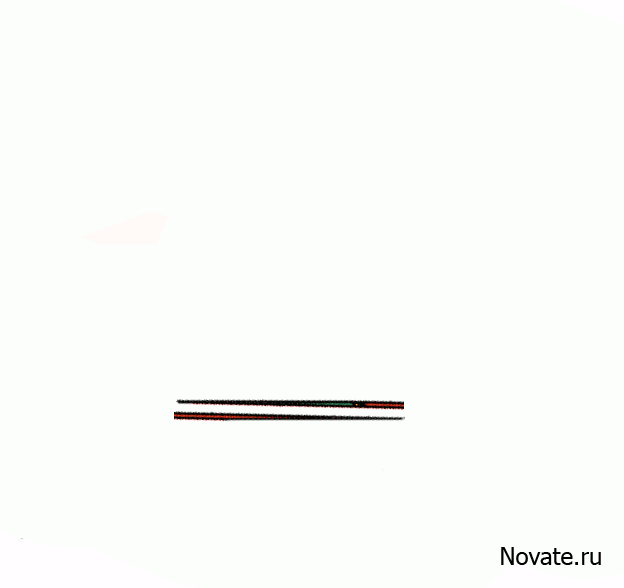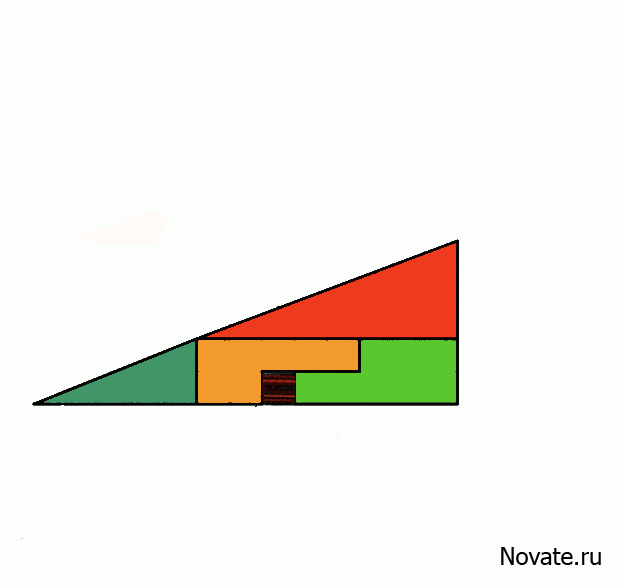
В действительности это не оптический обман, а интересная задача. Площади закрашенных фигур, разумеется, равны между собой (32 клетки), однако, то, что визуально наблюдается как треугольники 13×5, на самом деле таковым не является, и имеет разные площади (S13×5 = 32,5 клетки). То есть ошибка, замаскированная в условии задачи, состоит в том, что начальная фигура поименована треугольником (на самом деле это — вогнутый 4-угольник). Это отчётливо заметно на рисунке-схеме ниже — «гипотенузы» верхней и нижней фигур проходят через разные точки: (8,3) вверху и (5,2) — внизу. Секрет в свойствах синего и красного треугольников. Это легко проверить вычислениями.

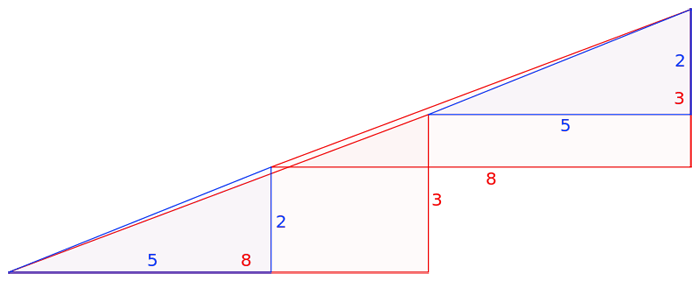
Отношения длин соответствующих сторон синего и красного треугольников не равны друг другу (2/3 и 5/8), поэтому эти треугольники не являются подобными, а значит, имеют разные углы при соответствующих вершинах. Назовём первую фигуру, являющуюся вогнутым четырёхугольником, и вторую фигуру, являющуюся вогнутым восьмиугольником, псевдотреугольниками. Если нижние стороны этих псевдотреугольников параллельны, то гипотенузы в обоих псевдотреугольниках 13×5 на самом деле являются ломаными линиями (на верхнем рисунке создаётся излом внутрь, а на нижнем — наружу). Если наложить верхнюю и нижнюю фигуры 13×5 друг на друга, то между их «гипотенузами» образуется параллелограмм, в котором и содержится «лишняя» площадь. На рисунке-схеме этот параллелограмм приведён в верных пропорциях.

Острый угол в этом параллелограмме равен arcctg 46 ≈ 0°1′18,2″. На такой угол минутная стрелка на исправных часах сдвигается за 12,45 с. Именно на такую величину тупой угол в рассматриваемом параллелограмме отличается от развёрнутого. Визуально столь ничтожное отличие незаметно, зато оно хорошо просматривается на анимации.

По словам Мартина Гарднера, эту задачу изобрёл иллюзионист-любитель из Нью-Йорка Пол Карри в 1953. Однако принцип, заложенный в неё, был известен ещё в 1860-е годы. Можно заметить, что длины сторон фигур из данной задачи (2, 3, 5, 8, 13) являются последовательными числами Фибоначчи.

Любителей голосок наверняка порадуют еще 16 увлекательных задачек на внимательность и логику.